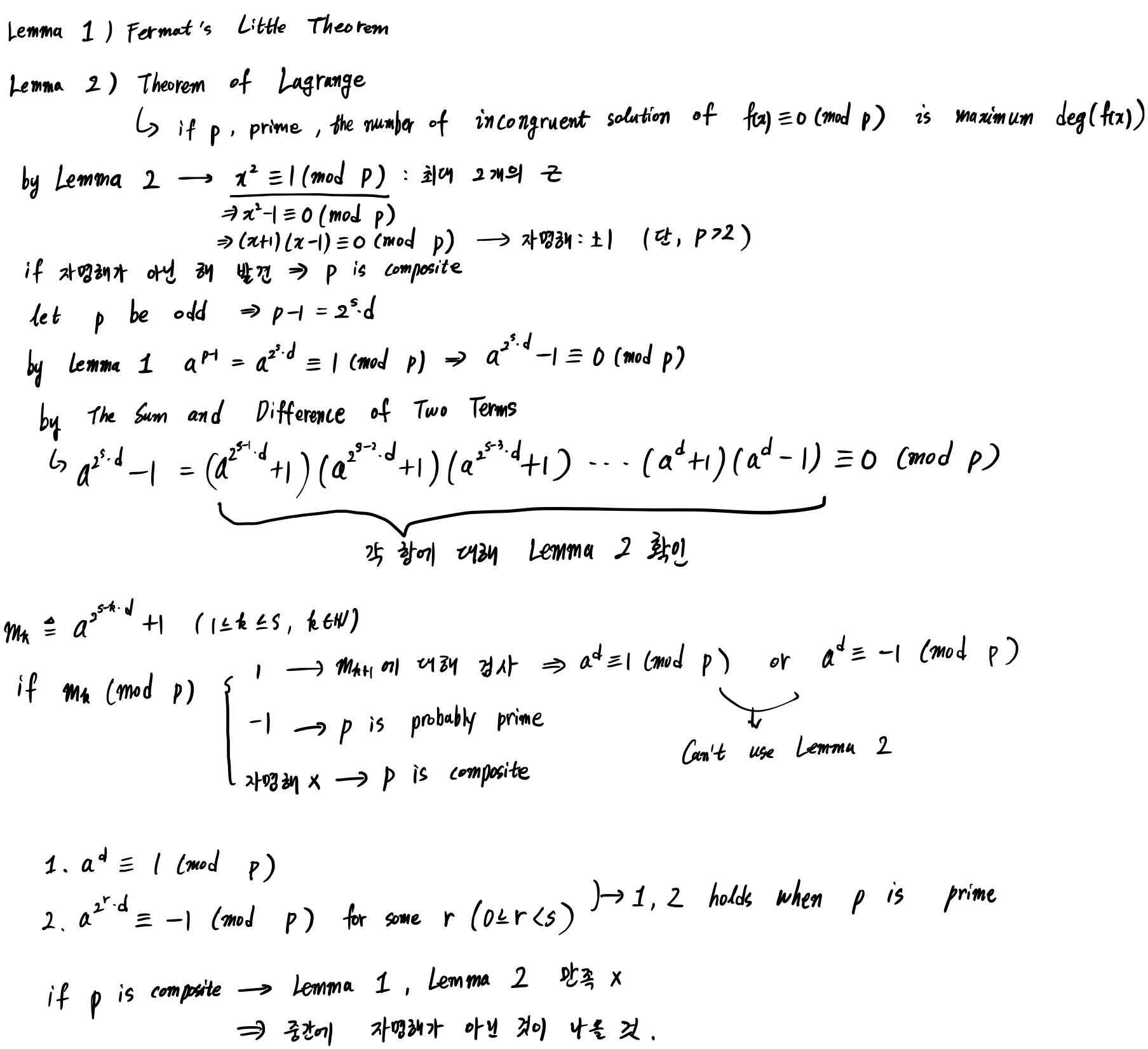이 글을 읽기 전 알아야 할 내용 (하단 더보기 클릭)
본 내용을 시작하기에 앞서 학습되어 있어야 할 내용은 정수론에서 합동식의 개념과 성질에 관한 것과 Big-O 표기법에 대한 내용입니다.
Big-O 표기법에 대한 내용은 아래 링크를 통해 보실 수 있고, 합동식에 관한 내용은 추후에 업로드 예정이나, 일정을 잡지 못하여 업로드 하는대로 Big-O 표기법과 같이 링크를 달아두로록 하겠습니다. (그 전까지는 다른 것을 보고 학습한 후 이 글을 읽는 것을 추천합니다.) 또한 라그랑주 정리와 관련해서는 추후에 업로드 하도록 하겠습니다.
밀러-라빈 소수 판별법은 주어진 수가 소수인지 아닌지 판별하는 알고리즘으로, 확률적 알고리즘이다. 이것이 확률적 알고리즘이라고 하는 것은 주어진 수가 "합성수"이거나 "아마도 소수일 것이다"라고 판단해 주기 때문이다.
밀러-라빈을 이해하기 위해서는 정수론에 대한 이해가 필요한데, 그 중에서도 특히 이 이론의 보조정리인 "페르마의 소정리"를 알고 있어야 한다.
Fermat's Little Theorem(페르마의 소정리)
정의
어떤 수가 소수일 간단한 필요 조건에 대한 정리이다. 즉, 소수이면 페르마의 소정리를 만족하지만 페르마의 소정리를 만족하는 정수라고 무조건 "소수이다"라고 단정지을 수는 없다. 즉, 모든 소수가 만족시키는 필요조건이지, 충분조건이 아니다.
페르마의 소정리를 만족하면서 소수가 아닌 수를 우리는 카마이클 수라고 부른다.
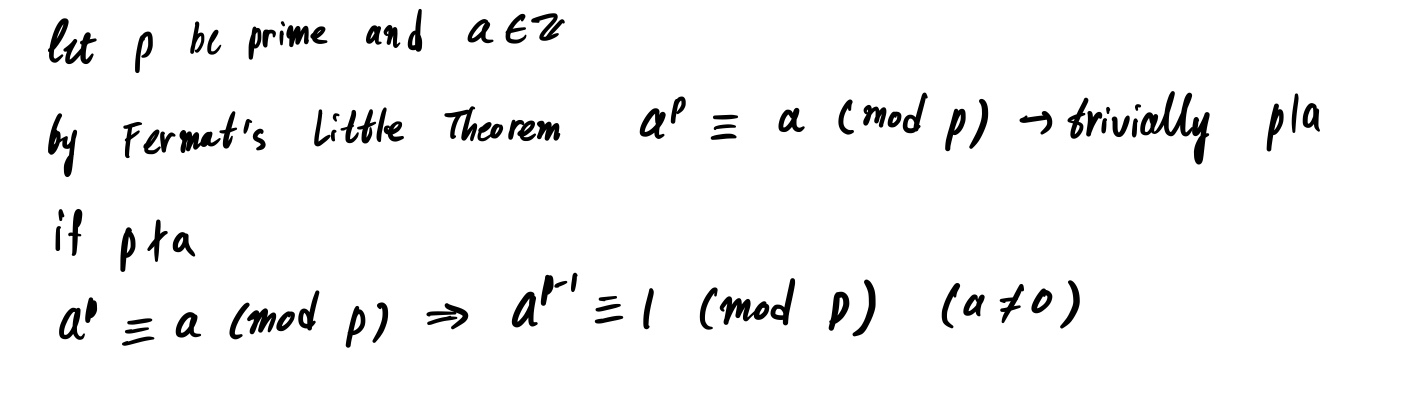
증명
Miller-Rabin Primality Test(밀러-라빈 소수판별법)
밀러-라빈 소수판별법은 소수인지 검사할 숫자를 입력하면 그것이 합성수이면 합성수인 것을, 소수이면 "아마 소수일 것 같다"는 것을 반환하게 된다. 이는 밀러-라빈 소수판별법이 결정적 알고리즘이 아닌, 확률적 알고리즘이기 때문이다.
알고리즘
입력:
n: 소수인지 검사할 숫자
k: 소수판별법을 몇 회 실행할 것인지를 결정하는 숫자
출력:
n이 합성수이면 합성수이다.
아니면 아마 소수일 것 같다는 것 반환
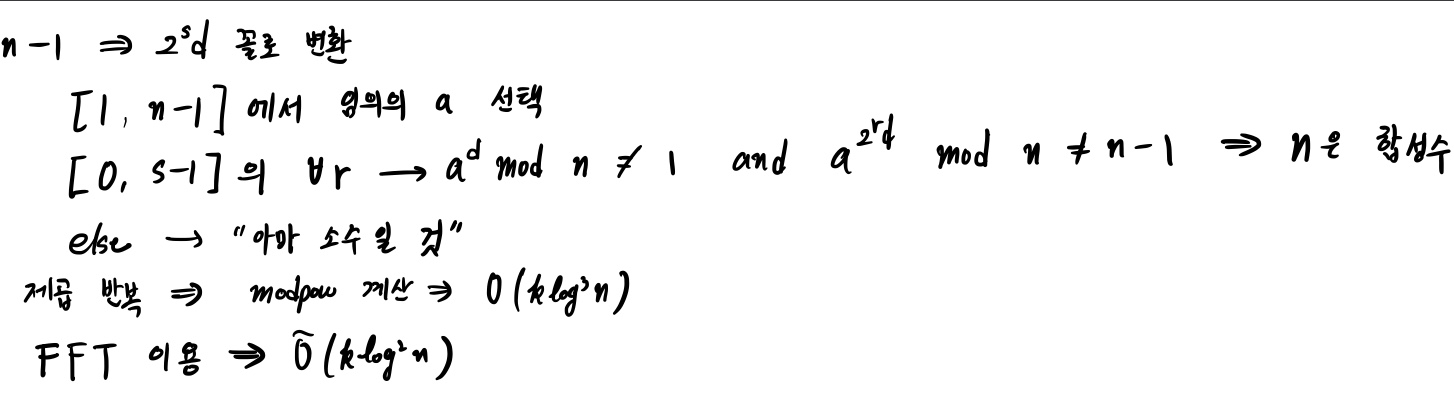
증명
간단한 구현
// find trivial solution - calculating a^(n-1) with power function
long long modpow(long long a, long long n, long long p)
{
long long ans = 1;
a %= p;
while(n){
if(n % 2) ans = (ans * a) % p;
n /= 2;
a = (a * a) % p; // to avoid overflow
}
return ans;
}
// miller-rabin
bool miller_rabin(long long p, long long a)
{
if(a % p == 0) return false;
long long k = p-1; // k = p-1 = 2^s*d
while(1){
long long tmp = modpow(a, k, p); // tmp is trivial solution
if(tmp == p-1) return true; // a^k = -1 (mod p)
if(k%2) return (tmp == 1 or tmp == p-1); // if k is odd
k /= 2;
}
}관련 문제: https://www.acmicpc.net/problem/5615
5615번: 아파트 임대
첫째 줄에 아파트의 면적의 수 N이 주어진다. 다음 줄부터 N개 줄에 카탈로그에 적혀있는 순서대로 면적이 주어진다. N은 100,000이하이고 면적은 231-1이하인 양의 정수이다.
www.acmicpc.net
알고리즘
적당한 소수 배열을 만들어서 밀러-라빈 소수 판별법을 수행한다. 여기서 적당한 소수 배열을 만드는 이유는 위에서 언급한 페르마의 소정리로써 유도되는 밀러-라빈 소수 판별법의 식에서의 a의 값을 위함이고(저기서 a는 양의 정수이면 가능하다), 또한 판별할 자연수와 그 배열의 값을 비교하여 조기종료를 함으로써 알고리즘의 소요 시간을 줄이기 위함이다.
문제에서 아파트 방의 면적을 살펴보자. 면적이 2xy + x + y라고 되어 있는 것을 알 수 있다. 이 식을 s라고 할 때 이것의 인수분해 꼴을 생각해보면 다음과 같이 식을 변형할 수 있음을 알 수 있다. → (2x+1)(2y+1) = (2s+1)
문제 조건에서 x와 y는 양의 정수이므로, 2x+1과 2y+1은 모두 홀수 이며, 그 두 수의 곱은 소수가 될 수 없다. 따라서 이 문제를 풀 때 2x+1과 2y+1에 대해서 이 둘을 곱한 값이 소수인지의 여부를 판별하면 된다. 즉, 주어지는 수가 아파트의 면적이므로, 이를 s라 했을 때 2s+1이 소수인지 여부를 판별하면 되는 것이다.
이에 대한 소스코드는 하단에 접은 글로 쓰여있다.
소스 코드
// BOJ 5615
#include <iostream>
#define ull unsigned long long
using namespace std;
ull alist[3] = {2, 7, 61}; // prime list for checking miller-rabin
// find trivial solution - calculating a^(n-1) with power function
long long modpow(ull a, ull n, ull p)
{
ull ans = 1;
a %= p;
while(n){
if(n % 2) ans = (ans * a) % p;
n /= 2;
a = (a * a) % p; // to avoid overflow
}
return ans;
}
// miller-rabin
bool miller_rabin(ull p, ull a)
{
if(a % p == 0) return false;
ull k = p-1; // k = p-1 = 2^s*d
while(1){
ull tmp = modpow(a, k, p); // tmp is trivial solution
if(tmp == p-1) return true; // a^k = -1 (mod p)
if(k%2) return (tmp == 1 or tmp == p-1); // if k is odd
k /= 2;
}
}
// checking whether n is prime or not
bool isprime(ull n)
{
if(n<2) return false; // if n is 1
if(n<4) return true; // if n is 2, 3
for(int i=0; i<3; i++){
ull a = alist[i]; // a is one of the elements among alist
if(n == a) return true; // if n = a, it means that n is prime
if(!miller_rabin(n, a)) return false;
}
return true;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ull n, s; // n is the number of testcase and s is space of the room
ull cnt = 0;
cin >> n;
for(int i=0; i<n; i++){
cin >> s; // s = 2xy + x + y -> (2x+1)*(2y+1) = (2s+1)
if(isprime(2*s+1)) cnt++; // checking if 2s+1 is prime or not -> if 2s+1 is prime, count the number of it
}
cout << cnt;
return 0;
}